Prechall
- Catégorie: Cracking et programming
- Date de résolution : 11/04/2025
- URL : https://fcsc.fr/teasing
Epreuve 1/3
Enoncé
"Il semblerait que cette broderie ait été interrompue.
Saurez-vous reconstituer la fin de cette broderie à partir d'une image disque de la mémoire de cette machine à broder ?"

On commence par le décompresser :
$ xd -d embroidery-usbdisk.img.xz
Puis on a un fichier .img qu'il convient de mount pour récupérer un fichier : fcsc.exp
Après une recherche web, je trouve ce site : joshvarga
Et tada...

on file voir l'URL brodée et on a le premier flag :
FCSC{ab983f8a573e4f7e84bc03ebff5a4c349273c29196c0efa0dff00b5128ad97e1}
Epreuve 2/3
Enoncé
"Vous avez trouvé un ESP32 dans une poubelle.
Après vous être branché sur le port série, il semble qu'il attend un flag.
Vous arrivez à dumper sa mémoire flash, pourrez-vous retrouver le flag ?
Un fichier extension.elf est fourni
Premières analyses
1$ readelf -h extension.elf
2ELF Header:
3 Magic: 7f 45 4c 46 01 01 01 00 00 00 00 00 00 00 00 00
4 Class: ELF32
5 Data: 2's complement, little endian
6 Version: 1 (current)
7 OS/ABI: UNIX - System V
8 ABI Version: 0
9 Type: EXEC (Executable file)
10 Machine: Tensilica Xtensa Processor
11 Version: 0x1
12 Entry point address: 0x400812bc
13 Start of program headers: 52 (bytes into file)
14 Start of section headers: 353392 (bytes into file)
15 Flags: 0x300
16 Size of this header: 52 (bytes)
17 Size of program headers: 32 (bytes)
18 Number of program headers: 6
19 Size of section headers: 40 (bytes)
20 Number of section headers: 27
21 Section header string table index: 26
Il s'agit bien d'un fichier ELF ESP32/Xtensa
Je pars direct en analyse statique avec ghidra 👀
Parcours des fonctions en partant de : main_task -> app_main -> checkflag -> verif
Interessons nous à verif
1byte verif(int input)
2
3{
4 byte rc;
5 uint j;
6 int iVar1;
7 int length;
8 uint temp;
9 uint i;
10 uint state;
11 byte buffer [80]; //Une taille de 48 aurait été suffisante...
12 byte xor_result;
13
14 length = strlen(input);
15 if (length == 0x18) { //Longueur de l'argument = 24
16 for (length = 0; length < 0x18; length = length + 1) {
17 buffer[length] = 0;
18 }
19 // Données générées dans buffer[0..23] (après appel de cette fonction)
20 //uint8_t buffer[24] = {
21 // 0x7f, 0x42, 0xf9, 0xaa, 0x83, 0x51, 0x33, 0xfd,
22 // 0x9e, 0xdd, 0xa9, 0x14, 0x69, 0x31, 0xe7, 0xb1,
23 // 0x21, 0xba, 0xde, 0x3e, 0x2c, 0x6b, 0x2b, 0xc8
24 //};
25 length = 0;
26 state = 0x7f;
27 while (length < 0xc0) { // Fonction qui initialise les 24 premiers int de buffer
28 for (i = 0; (int)i < 8; i = i + 1) {
29 temp = state & 0x71;
30 for (j = 1; (int)j < 8; j = j + 1) {
31 temp = (temp ^ (int)(state & 0x71) >> (j & 0x1f)) & 0xff;
32 }
33 iVar1 = length + 7;
34 if (-1 < length) {
35 iVar1 = length;
36 }
37 buffer[iVar1 >> 3] = buffer[iVar1 >> 3] ^ (byte)((state & 1) << 0x20 - (0x20 - (i & 0x1f)));
38 state = state >> 1 | (temp & 1) << 7;
39 length = length + 1;
40 }
41 }
42 //Données dans &DAT_3f403840
43 //uint8_t data[24] = {
44 // 0x39, 0x02, 0x18, 0x06, 0xF8, 0x66, 0x27, 0x7B,
45 // 0x76, 0x2A, 0x69, 0x26, 0x35, 0x35, 0x75, 0x69,
46 // 0x70, 0x45, 0x3E, 0x0D, 0x19, 0x1A, 0x6B, 0xB5
47 //};
48
49 memcpy(buffer + 0x18,&DAT_3f403840,0x18); //On copie les valeurs de data dans buffer[24..47]
50 breakpoint(0x1000,0x400d88a2,1,1); //Pourquoi ça ?
51 rc = 0;
52 for (length = 0; length < 0x18; length = length + 1) {
53 xor_result = buffer[length] ^ buffer[length + 0x18]; //On xor 2 à 2 les 24 premiers int de buffer avec les 24 derniers
54 buffer[length + 0x18] = xor_result;
55 rc = rc | xor_result ^ *(byte *)(input + length); // On compare avec la saisie de input !
56 }
57 rc = rc | buffer[24] != 'F' | buffer[25] != 'C' | buffer[26] != 'S' | buffer[27] != 'C'; //On verifie les 4 premiers chars
58 }
59 else {
60 rc = 1;
61 }
62 return rc;
63}
Donc, verif fait ceci :
- Vérifie la taille de l'argument input qui doit être égal à 24 octets
- Calcule bit à bit 24 octets dans buffer[0..23]
- Load 24 octets depuis l'adresse 0x3f403840 dans buffer[24..47]
- break ???
- XOR buffer avec buffer[x+24]
- Ecris le résultat du XOR dans buffer[24..47]
- Compare les 4 premiers octets avec 'FCSC'
Exploit
Et c'est parti pour le XOR avec les octets trouvés
1#include <stdio.h>
2#include <stdint.h>
3
4int main() {
5 // Octets générés au debut de verif
6 uint8_t buffer1[24] = {
7 0x7f, 0x42, 0xf9, 0xaa, 0x83, 0x51, 0x33, 0xfd,
8 0x9e, 0xdd, 0xa9, 0x14, 0x69, 0x31, 0xe7, 0xb1,
9 0x21, 0xba, 0xde, 0x3e, 0x2c, 0x6b, 0x2b, 0xc8
10 };
11
12 // Données constantes contenues à l'adresse 0x3f403840
13 const uint8_t buffer2[24] = {
14 0x39, 0x03, 0xB2, 0xEF, 0xF8, 0x0E, 0x71, 0xB4,
15 0xDB, 0x93, 0xF6, 0x51, 0x3A, 0x62, 0xA6, 0xE8,
16 0x64, 0x9B, 0x81, 0x04, 0x01, 0x42, 0x74, 0xB5
17 };
18
19 // Calculer l'entrée attendue
20 uint8_t input[24];
21 for (int i = 0; i < 24; i++) {
22 input[i] = buffer1[i] ^ buffer2[i];
23 printf("%c", input[i]);
24 }
25
26 return 0;
27}
On compile et on exécute :
1$ ./reverse
2FAKE{_BIEN_ESSAYE!_:-)_}
Hum ! 🤔 On a du oublié quelquechose...Bien sûr, ce flag ne valide pas !
Et c'est là où, perso, j'ai passé plusieurs heures à comprendre... L'architecture Xtensa gère des interruptions au niveau du code ASM directement et c'est précisément le rôle de l'instruction break qui se trouve dans le code juste après le memcpy... Voici le lien vers la doc officielle
Et dans cette doc, on peut y lire :
Interrupt Levels
| Level | Symbol | Remark |
|---|---|---|
| 1 | N/A | Exception and level 0 interrupts. Handled by ESP-IDF |
| 2-3 | N/A | Medium level interrupts. Handled by ESP-IDF |
| 4 | xt_highint4 | Free to use (See 1) |
| 5 | xt_highint5 | Normally used by ESP-IDF debug logic (See 1) |
| NMI | xt_nmi | Free to use |
| dbg | xt_debugexception | Debug exception. Called on e.g. a BREAK instruction. (See 2) |
La dernière ligne semble prometteuse 👀 (=dbg)
Allons voir le code de xt_debugexception
1void xt_debugexception(undefined *param_1)
2
3{
4 *param_1 = *param_1;
5 param_1[1] = param_1[1] ^ 2;
6 param_1[2] = param_1[2] ^ 0x18;
7 param_1[3] = param_1[3] ^ 6;
8 param_1[4] = param_1[4];
9 param_1[5] = param_1[5] ^ 0x66;
10 param_1[6] = param_1[6] ^ 0x27;
11 param_1[7] = param_1[7] ^ 0x7b;
12 param_1[8] = param_1[8] ^ 0x76;
13 param_1[9] = param_1[9] ^ 0x2a;
14 param_1[10] = param_1[10] ^ 0x69;
15 param_1[0xb] = param_1[0xb] ^ 0x26;
16 param_1[0xc] = param_1[0xc] ^ 0x35;
17 param_1[0xd] = param_1[0xd] ^ 0x35;
18 param_1[0xe] = param_1[0xe] ^ 0x75;
19 param_1[0xf] = param_1[0xf] ^ 0x69;
20 param_1[0x10] = param_1[0x10] ^ 0x70;
21 param_1[0x11] = param_1[0x11] ^ 0x45;
22 param_1[0x12] = param_1[0x12] ^ 0x3e;
23 param_1[0x13] = param_1[0x13] ^ 0xd;
24 param_1[0x14] = param_1[0x14] ^ 0x19;
25 param_1[0x15] = param_1[0x15] ^ 0x1a;
26 param_1[0x16] = param_1[0x16] ^ 0x6b;
27 param_1[0x17] = param_1[0x17];
28 return;
29}
Bingo ! Au call break, xt_debugexception modifie les octets de notre buffer en faisant un XOR avec de nouveaux octets... 👊
Modification de notre reverse.c :
1#include <stdio.h>
2#include <stdint.h>
3
4int main() {
5 // Octets générés au debut de verif
6 uint8_t buffer1[24] = {
7 0x7f, 0x42, 0xf9, 0xaa, 0x83, 0x51, 0x33, 0xfd,
8 0x9e, 0xdd, 0xa9, 0x14, 0x69, 0x31, 0xe7, 0xb1,
9 0x21, 0xba, 0xde, 0x3e, 0x2c, 0x6b, 0x2b, 0xc8
10 };
11
12 // Données constantescontenues à l'adresse 0x3f403840
13 const uint8_t buffer2[24] = {
14 0x39, 0x03, 0xB2, 0xEF, 0xF8, 0x0E, 0x71, 0xB4,
15 0xDB, 0x93, 0xF6, 0x51, 0x3A, 0x62, 0xA6, 0xE8,
16 0x64, 0x9B, 0x81, 0x04, 0x01, 0x42, 0x74, 0xB5
17 };
18
19 uint8_t xt_debugexception[24] = {
20 0x00, 0x02, 0x18, 0x06, 0x00, 0x66, 0x27, 0x7B,
21 0x76, 0x2A, 0x69, 0x26, 0x35, 0x35, 0x75, 0x69,
22 0x70, 0x45, 0x3E, 0x0D, 0x19, 0x1A, 0x6B, 0x00
23 };
24
25 // Calculer l'entrée attendue
26 uint8_t input[24];
27 for (int i = 0; i < 24; i++) {
28 input[i] = buffer1[i] ^ buffer2[i] ^ xt_debugexception[i];
29 printf("%c", input[i]);
30 }
31
32 return 0;
33}
1$ ./reverse
2FCSC{9e23d6cff405da7434}
Deuxième flag !
FCSC{9e23d6cff405da7434}
Epreuve 3/3
Enoncé
"Voici un super sudoku hexadécimal. Vous devez résoudre ce sudoku en plaçant un caractère hexadécimal (entre 0 et f) dans chaque case, en respectant les contraintes classiques des sudokus : les caractères hexadécimaux d'une même ligne, d'une même colonne ou d'un même carré surligné doivent être tous différents.
Les diaboliques concepteurs, fidèles à leur mesquinerie traditionnelle, ont cependant ajouté une contrainte supplémentaire. Vous devez fournir la solution qui maximise le PGCD des 16 lignes, interpretées comme des nombres hexadécimaux de 16 caractères (donc, compris entre 0 et 16^16 - 1). Par exemple, la ligne 0 1 2 3 4 5 6 7 8 9 a b c d e f est représentée par l'entier 0x0123456789abcdef.
Une fois la grille complétée, concaténez toutes les lignes de haut en bas, et encadrez le résultat S dans FCSC{} (par exemple si la concaténation des lignes donne S = 1234abcd, le flag serait FCSC{1234abcd}).
Bonne chance ! "

Premières analyses
Avec seulement 12 valeurs préremplies, il existe des millions de solutions. Perso, j'ai laissé mon solver tourné 24h, et je suis arrivé à +10M de solutions.
Sur toutes ces grilles, le max(pgcd) était 15 ! 🤔
Il faut donc appliquer une approche Think different
Nous cherchons à maximiser le PGCD de toutes les lignes et notre objectif est de réfléchir à cet objectif uniquement et pas à résoudre le sudoku.
Quels sont les propriétés d'un sudoku et comment les appliquer pour trouver le plus grand facteur ?
Pour chaque sudoku, une propriété nous intéresse particulièrement, c'est que la somme des lignes est un multiple de 1111111111111111. Le saviez vous ? 💡
Et pour un hexadoku, cette valeur est : S = 0x7fffffffffffffff8
Pour trouver S, il faut additionner 1..f = (16*15)/2 =120 et additionner 120*10e15 + 120*10e14 + .... + 120*10e1 + 120...
Autre propriété mathématique intéressante : si un facteur est commun aux 16 nombres, celui ci sera aussi un facteur de la somme de ces nombres !
Il reste donc à trouver le plus grand facteur de S qui correspond.
Exploit
Commencons par calculer les facteurs de S :
1def find_factors(n):
2 divisors = set()
3 for i in range(1, int(math.sqrt(n)) + 1):
4 if n % i == 0:
5 divisors.add(i)
6 divisors.add(n // i)
7 return sorted(divisors, reverse=True)
1$ find_factors S
2factors = [147573952589676412920, 73786976294838206460, 49191317529892137640, 36893488147419103230, 29514790517935282584, 24595658764946068820, 18446744073709551615, 14757395258967641292, 12297829382473034410, 9838263505978427528, 8680820740569200760, 7378697629483820646, 6148914691236517205, 4919131752989213764, 4340410370284600380, 3689348814741910323, 2893606913523066920, 2459565876494606882, 2170205185142300190, 1736164148113840152, 1446803456761533460, 1229782938247303441, 1085102592571150095, 868082074056920076, 723401728380766730, 578721382704613384, 574217714356717560, 434041037028460038, 361700864190383365, 289360691352306692, 287108857178358780, 230224575022896120, 217020518514230019, 191405904785572520, 144680345676153346, 143554428589179390, 115112287511448060, 114843542871343512, 95702952392786260, 76741525007632040, 72340172838076673, 71777214294589695, 57556143755724030, 57421771435671756, 47851476196393130, 46044915004579224, 38370762503816020, 38281180957114504, 33777512609218680, 28778071877862015, 28710885717835878, 23925738098196565, 23022457502289612, 19185381251908010, 19140590478557252, 16888756304609340, 15348305001526408, 14355442858917939, 13542622060170360, 11511228751144806, 11259170869739560, 9592690625954005, 9570295239278626, 8444378152304670, 7674152500763204, 6771311030085180, 6755502521843736, 5755614375572403, 5629585434869780, 4785147619639313, 4514207353390120, 4222189076152335, 3837076250381602, 3385655515042590, 3377751260921868, 2814792717434890, 2708524412034072, 2257103676695060, 2251834173947912, 2251765454471160, 1918538125190801, 1692827757521295, 1688875630460934, 1407396358717445, 1354262206017036, 1128551838347530, 1125917086973956, 1125882727235580, 902841470678024, 895815467015160, 844437815230467, 750588484823720, 677131103008518, 564275919173765, 562958543486978, 562941363617790, 451420735339012, 450353090894232, 447907733507580, 375294242411860, 338565551504259, 298605155671720, 281479271743489, 281470681808895, 225710367669506, 225176545447116, 223953866753790, 187647121205930, 179163093403032, 150117696964744, 149302577835860, 132456791439480, 112855183834753, 112588272723558, 111976933376895, 93823560602965, 89581546701516, 75058848482372, 74651288917930, 66228395719740, 59721031134344, 56294136361779, 52695027471480, 44790773350758, 44152263813160, 37529424241186, 37325644458965, 33114197859870, 29860515567172, 26491358287896, 26347513735740, 22395386675379, 22076131906580, 22024592288760, 18764712120593, 17565009157160, 16557098929935, 14930257783586, 13245679143948, 13173756867870, 11038065953290, 11012296144380, 10539005494296, 8830452762632, 8782504578580, 8761733285880, 7465128891793, 7341530762920, 6622839571974, 6586878433935, 5519032976645, 5506148072190, 5269502747148, 4415226381316, 4404918457752, 4391252289290, 4380866642940, 3670765381460, 3513001831432, 3512894624760, 3311419785987, 2920577761960, 2753074036095, 2634751373574, 2207613190658, 2202459228876, 2195626144645, 2190433321470, 1835382690730, 1756500915716, 1756447312380, 1752346657176, 1468306152584, 1460288880980, 1317375686787, 1295564252280, 1170964874920, 1103806595329, 1101229614438, 1095216660735, 917691345365, 878250457858, 878223656190, 876173328588, 734153076292, 730144440490, 702578924952, 647782126140, 585482437460, 584115552392, 550614807219, 515396075640, 439125228929, 439111828095, 438086664294, 431854750760, 367076538146, 365072220245, 351289462476, 323891063070, 292741218730, 292057776196, 259112850456, 257698037820, 234192974984, 219043332147, 215927375380, 206640860280, 183538269073, 175644731238, 171798691880, 161945531535, 146370609365, 146028888098, 129556425228, 128849018910, 117096487492, 107963687690, 103320430140, 103079215128, 87822365619, 86370950152, 85899345940, 85698802680, 73014444049, 68880286760, 64778212614, 64424509455, 58548243746, 53981843845, 51660215070, 51539607564, 43185475076, 42949672970, 42849401340, 41328172056, 34440143380, 34359738376, 34359738360, 32389106307, 29274121873, 28566267560, 25830107535, 25769803782, 21592737538, 21474836485, 21424700670, 20664086028, 17220071690, 17179869188, 17179869180, 17139760536, 14283133780, 13776057352, 13668850680, 12884901891, 11453246120, 10796368769, 10712350335, 10332043014, 8610035845, 8589934594, 8589934590, 8569880268, 7141566890, 6888028676, 6871947672, 6834425340, 5726623060, 5713253512, 5166021507, 5041106040, 4556283560, 4294967297, 4294967295, 4284940134, 3570783445, 3444014338, 3435973836, 3417212670, 2863311530, 2856626756, 2733770136, 2520553020, 2290649224, 2278141780, 2142470067, 2021161080, 1722007169, 1717986918, 1708606335, 1680368680, 1431655765, 1428313378, 1366885068, 1260276510, 1145324612, 1139070890, 1010580540, 1008221208, 911256712, 858993459, 840184340, 804050040, 714156689, 683442534, 673720360, 630138255, 572662306, 569535445, 505290270, 504110604, 455628356, 420092170, 404232216, 402025020, 341721267, 336860180, 336073736, 336063480, 286331153, 268016680, 252645135, 252055302, 227814178, 210046085, 202116108, 201012510, 168430090, 168036868, 168031740, 160810008, 134744072, 134008340, 133695480, 126027651, 113907089, 112021160, 101058054]
En prenant ces facteurs du plus grand au plus petit, si pour l'un d'entre eux, il existe au moins 16 variants (multiple de ce facteur inférieur à S) dont la représentation hexadécimale du nombre contient tous les caractères '0123456789abcdef', cela fait de lui un bon candidat pour notre problème...
Calculons ça !
1import math
2from collections import Counter
3
4def is_valid_number(num,ref):
5 digits = Counter(str(num))
6 check = Counter(str(ref))
7 return digits == check
8
9def find_variants(num,max):
10 candidate = num
11 variants = []
12 factor = 1
13 while candidate <= max:
14 candidate_hex = f"{candidate:016x}"
15 if is_valid_number(candidate_hex,'0123456789abcdef'):
16 variants.append(candidate)
17 candidate += num
18 factor += 1
19 return variants
20
21S = 0x7fffffffffffffff8
22factors = [147573952589676412920, ...]
23
24for factor in factors:
25 candidates = find_variants(factor,S)
26 print(f"factor {factor:016x} has {len(candidates)} candidates : ")
27 if len(candidates) > 15 :
28 for candidate in candidates :
29 print(f" {candidate:016x}")
1totoiste@server:~/hacking$ python3 variant.py
2factor 7fffffffffffffff8 has 0 candidates :
3factor 3fffffffffffffffc has 0 candidates :
4factor 2aaaaaaaaaaaaaaa8 has 0 candidates :
5factor 1fffffffffffffffe has 0 candidates :
6factor 19999999999999998 has 0 candidates :
7factor 15555555555555554 has 0 candidates :
8factor ffffffffffffffff has 0 candidates :
9factor cccccccccccccccc has 0 candidates :
10factor aaaaaaaaaaaaaaaa has 0 candidates :
11factor 8888888888888888 has 0 candidates :
12factor 7878787878787878 has 0 candidates :
13factor 6666666666666666 has 0 candidates :
14factor 5555555555555555 has 0 candidates :
15factor 4444444444444444 has 0 candidates :
16factor 3c3c3c3c3c3c3c3c has 0 candidates :
17factor 3333333333333333 has 0 candidates :
18factor 2828282828282828 has 0 candidates :
19factor 2222222222222222 has 0 candidates :
20factor 1e1e1e1e1e1e1e1e has 0 candidates :
21factor 1818181818181818 has 0 candidates :
22factor 1414141414141414 has 0 candidates :
23factor 1111111111111111 has 0 candidates :
24factor 0f0f0f0f0f0f0f0f has 0 candidates :
25factor 0c0c0c0c0c0c0c0c has 0 candidates :
26factor 0a0a0a0a0a0a0a0a has 0 candidates :
27factor 0808080808080808 has 0 candidates :
28factor 07f807f807f807f8 has 0 candidates :
29factor 0606060606060606 has 0 candidates :
30factor 0505050505050505 has 0 candidates :
31factor 0404040404040404 has 0 candidates :
32factor 03fc03fc03fc03fc has 0 candidates :
33factor 0331ec07fcce13f8 has 2 candidates :
34factor 0303030303030303 has 0 candidates :
35factor 02a802a802a802a8 has 0 candidates :
36factor 0202020202020202 has 0 candidates :
37factor 01fe01fe01fe01fe has 0 candidates :
38factor 0198f603fe6709fc has 4 candidates :
39factor 0198019801980198 has 0 candidates :
40factor 0154015401540154 has 0 candidates :
41factor 0110a402a99a06a8 has 2 candidates :
42factor 0101010101010101 has 0 candidates :
43factor 00ff00ff00ff00ff has 0 candidates :
44factor 00cc7b01ff3384fe has 8 candidates :
45factor 00cc00cc00cc00cc has 0 candidates :
46factor 00aa00aa00aa00aa has 0 candidates :
47factor 00a3959b328f9d98 has 2 candidates :
48factor 0088520154cd0354 has 4 candidates :
49factor 0088008800880088 has 0 candidates :
50factor 0078007800780078 has 0 candidates :
51factor 00663d80ff99c27f has 16 candidates :
52 02cbae86fd345179
53 17902cbae86fd345
54 2cbae86fd3451790
55 34517902cbae86fd
56 4517902cbae86fd3
57 517902cbae86fd34
58 6fd34517902cbae8
59 7902cbae86fd3451
60 86fd34517902cbae
61 902cbae86fd34517
62 ae86fd34517902cb
63 bae86fd34517902c
64 cbae86fd34517902
65 d34517902cbae86f
66 e86fd34517902cba
67 fd34517902cbae86
On place ces candidats dans l'ordre idoine par rapport à la grille fournie et on obtient le 3ième flag
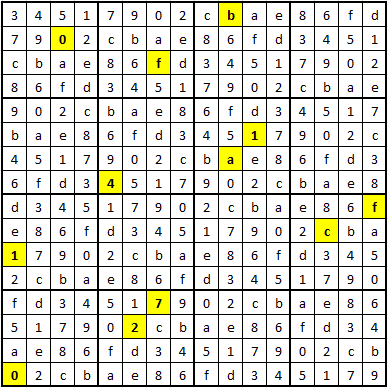
That's it !
FCSC{34517902cbae86fd7902cbae86fd3451cbae86fd3451790286fd34517902cbae902cbae86fd34517bae86fd 34517902c4517902cbae86fd36fd34517902cbae8d34517902cbae86fe86fd34517902cba17902cbae86fd3452cb ae86fd3451790fd34517902cbae86517902cbae86fd34ae86fd34517902cb02cbae86fd345179}